Manacher 算法求最长回文子串

发表于 2017-07-31 更新于 2024-09-20 Disqus：

背景

本文来源于leetcode上的一道求最长回文子串的中级算法题

先来个思路

由回文的性质想到，从回文的对称轴向两边同时扩张，在回文半径内，两边的字符一定是相同的。

因此，我们是否可以从左向右依次遍历字符串，用扩展的方法来找出所有的回文串，并记录最长的那一个呢?

说干就干，经过几次WA，终于AC了，代码如下：

func longestPalindrome(s string) string {
    i, j, max, current_len := 0,0,0,0
    var longest string
    n := len(s)

    for i = 0; i < n; i++ {
        for j = 0; i - j >= 0 && i + j < n; j++ { // if the length of the palindrome is odd  
            if s[i - j] != s[i + j] {
                break
            }
            current_len = j * 2 + 1
        }
        if current_len > max {
            max = current_len
            longest = s[i - j + 1: i + j]
        }
        for j = 0; i - j >= 0 && i + j + 1 < n; j++ { // for the even case  
            if s[i - j] != s[i + j + 1] {
                break
            }
            current_len = j * 2 + 2;
        }
        if current_len > max {
            max = current_len
            longest = s[i - j + 1: i + j + 1]
        }
    }
    return longest;
}

简单估计了下，长度为n的字符串，该思路的时间复杂度应该是O(n^2)级别的，而且，可以看到代码中需要分别处理奇偶长度的字符串，比较麻烦。

最最最关键的是，实在想不出其他的发子了。。。哈哈

manacher

经过一番搜索后，发现该问题大多数思路是使用 manacher算法，这个算法可以完美的解决奇偶问题，并且时间复杂度只有O(n)

解决奇偶单独处理的问题

由奇偶数的性质：奇数+偶数=奇数，因此假设我们的序列长度为奇数，我们在序列首尾和每个字符之间都添加一个字符#，则长度变为奇数，同理，长度为偶数时，如此处理后长度仍为奇数。

由此，通过添加一个额外的字符，就能解决序列长度特殊处理的问题。

算法实际流程

将问题简单化之后，接下来就要进入算法的核心流程了。

首先，manacher需要借助一个辅助数组p[i]，用来记录位置为i的字符的回文半径，因而字符串#a#b#a#d的p[i]则为：

1
2
3

处理后的字符串 |   # a # b # a # d #
p[i]          |   1 2 1 4 1 2 1 2 1
原始回文长度   |     1   3   1   1

可以看到，对于和原始字符串中对应位置的字符所在回文的长度，正好等于处理后的字符串的p[i] - 1

也就是说，只要求得了p[i]，就能获得最长的回文串

求`p[i]`

求p[i]的情况可以分为两种：

当前的字符处于未被遍历过的字符串
当前的字符处于已经被遍历过的字符串

对于情况1，由于没有历史数据可以借鉴，因此只能直接重新通过双向扩展来求回文半径

而对于情况2，如果我们不利用已经遍历过的回文的性质，那么算法就会和一开始的暴力遍历法一样低效，因此，这里需要仔细考虑如何利用回文性质快速求出会问半径p[i]

利用历史数据快速求解回文半径

假设之前已遍历的回文子串能延伸到达的最远位置为max，其所对应的对称轴为id，那么，对于上文的情况2，当前的字符c一定位于max的左边，并且可以利用回文的性质，通过c关于id的对称点j来求p[i]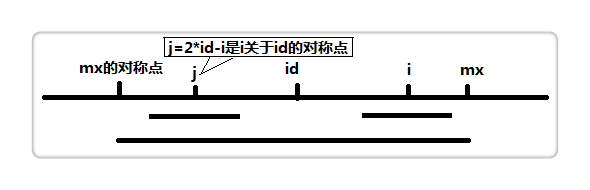

situation 2

因此，我们可以看到，回文半径的求解，分为以下几个情况：

j的回文包含在id的回文内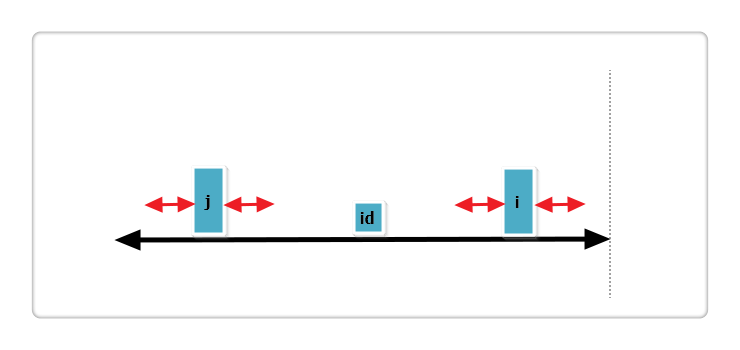

这种情况下，p[i] = p[j] = p[2*id - i]且p[i] < max - i
j的回文包含在id的回文外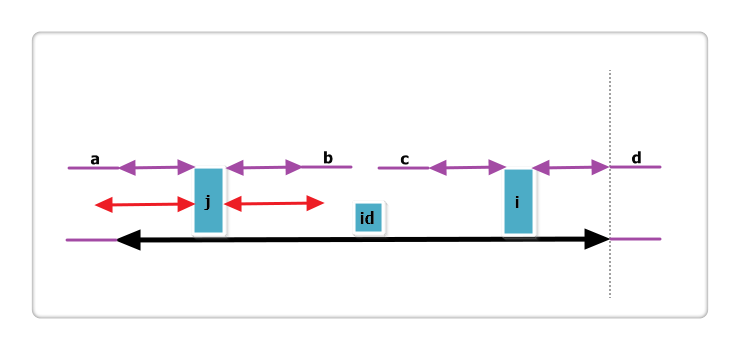

这种情况下，j的回文半径已经超出了id的半径，因此，我们需要推断i的回文半径是否也会超出

结论是：不会！

原因：假如j的回文包含a和b，且b等于c（b，c关于id对称），那么如果i的回文超过了max，则超过max的部分必定和j超出id左边回文半径有部分相等，这样，就会导致id的回文半径超出max，和已知条件矛盾，因此这是不可能的

此时，p[i] = max - i

综上所述，当p[i] < max - i时，p[i] = p[2*id - i]，而p[i] == max - i时，p[i] == max - i，因此可以得到，`p[i] = min(max - i, p[2*id - i])

最后，上代码

func min(a, b int) int {
    if a > b { 
        return b
    } else {
        return a
    }   
}

func longestPalindrome(s string) string {
    tmp := "#" + strings.Join(strings.Split(s,""),"#") + "#" 
    id, l, max, maxlen, mxpos := 0, len(tmp), 0, 0, 0
    p := make([]int, l)

    for i:=0; i<l; i++ {
        if max > i {
            p[i] = min(p[2*id - i], max - i)
        } else { 
            p[i] = 1
        }
        for ;i >= p[i] && i + p[i] < l && tmp[i-p[i]] == tmp[i+p[i]]; {
            p[i] += 1
        }
        if p[i] + i > max { 
            max  = p[i] + i
            id = i
        }
        if maxlen < p[i] {
            maxlen = p[i]
            mxpos = i
        }
    }
    return s[(mxpos+1-maxlen)/2:(mxpos-1+maxlen)/2]
}

参考资料

http://www.61mon.com/index.php/archives/181/

背景